死ぬほどカッコいい数学用語ランキング ベスト15

 

 

 

 

 

 

 

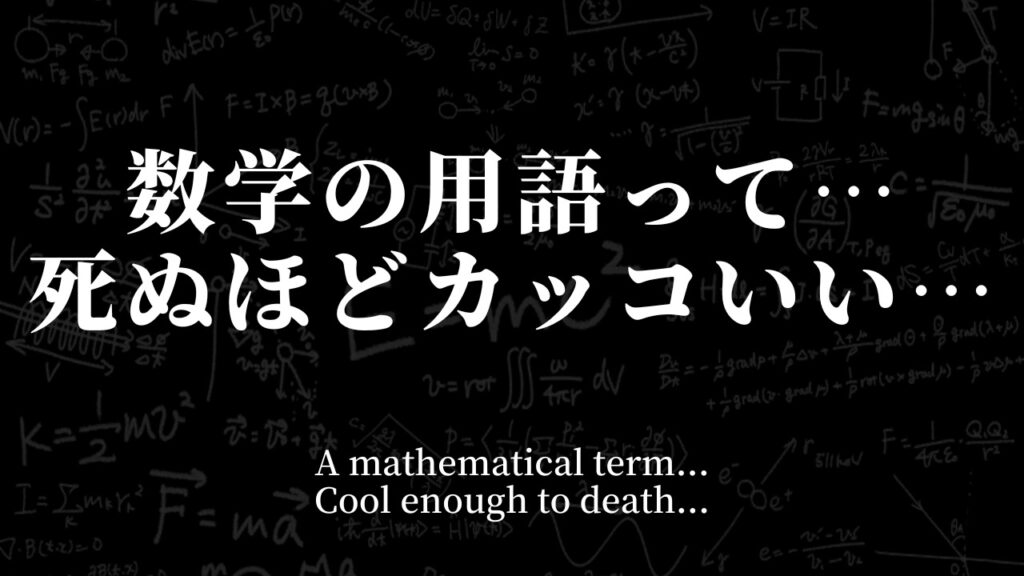
ご挨拶とレギュレーション

こんにちは。文系一筋30年、tdkです。

生まれた時から常々思ってたんですが、数学用語ってとってもカッコいいですよね。なのでランキングにしました。

とりあえず見てってください。

 

（僕が覚えている数学の最高峰）

キリ悪く15位から発表していきます。10じゃ足りなかったから。だってカッコよかったんだもの。

フェルマーの最終定理とかフィボナッチ数列なんてメジャーなものは一切出てきません。もし全部知ってる高学歴がいたらこんな記事読んでないで頼むから国の発展に尽力してくれと言いたい。

一部、物理用語と科学用語が混じってますがご了承ください。だってカッコよかったんだもの。

 

なお、画像は完全にイメージです。解説はWikipediaから引用。

ではいく。

 

第15位

ファンデルワールス力
［van der Waals force］

すみません、いきなり物理用語です。ドイツ語っぽい響きがカッコいい。vanがいいよvanが。

オランダ人のヨハネス・ファン・デル・ワールスさんが見つけたそう。

実在気体の状態方程式を定式化した際に導入された凝縮力であり、これによって分子間に形成される結合を、ファンデルワールス結合と言う。

？

 

第14位

ヤーコプスタール和
［Jacobsthal sum］

カタカナと漢字の組み合わせに加え、「和」で終わる変則的な感じがカッコいい。

ドイツのエルンスト・ヤーコプスタールさんが考えたそう。

ヤーコプスタール和とは、ガウス和と関連するルジャンドル記号の有限和である。

これがヤーコプスタール和だ！

？？

 

第13位

ハイパーボリック関数
［hyperbolic function］

近未来的な響きがカッコいい。日本語では双曲線関数と呼ぶそう。

高校で習ったサインコサインタンジェントの進化系みたいなやつらしい。わからない。もう何がわからないかがわからない。

（よくわからない解説）

ちなみにこれがハイパーボリック関数

？？？

 

第12位

チェビシェフの偏かたより
［Chebyshev’s bias］

偏かたよっちゃってるのがカッコいい。

ロシア人のパフヌティ・チェビシェフさんが発見したそう。さっきからまず名前がカッコいいのよ。これ発見したの鈴木さんだったら『鈴木の偏かたより』になってるからね。

あるNまでの素数には、4k + 3 の形をした素数（非ピタゴラス素数）が 4k + 1 の形をした素数（ピタゴラス素数）より多い現象のこと。

ピタゴラスイッチの話？

 

第11位

総虚体
［totally imaginary or totally complex］

シンプル漢字がカッコいい。日本語は短いのに、英語だと長いとこもカッコいい。

代数的整数論において、数体が総虚であるとは、実数体に埋め込めないことをいう。

全然分からん。

例えば、

例えば？

虚二次体、円分体、そしてより一般に、CM体などは総虚体である。

わからんて。殴るぞ。

 

第10位

ゴールドバッハ彗星
［Goldbach’s comet］

もうバッハがカッコいい。宇宙的な壮大な感じもカッコいい。

ドイツ人のクリスティアン・ゴールドバッハさんが言い始めたことらしく、様々な数学者があれこれ議論してるんだそう。

ゴールドバッハ彗星とは、所謂いわゆるゴールドバッハ関数 g(E) のプロットを指す名前である。

いわゆられてもわからん。

これがゴールドバッハ彗星だ！

わぁ！彗星だ！

綺麗！（文系の限界）

 

第9位

高立体選択的グリコシル化反応
［highly stereoselective glycosylation reaction］

科学用語です。漢字+カタカナ+漢字の並びがカッコいい。声に出して言いたいタイプ。

「高立体選択的グリコシル化反応」自体の説明が見つからなかったので、『グリコシル化反応』と『立体選択性』に分けてみました。

Q.グリコシル化反応ってなに。

タンパク質もしくは脂質へ糖類が付加する反応である。糖鎖付加とうさふかとも言う。この反応は、細胞膜の合成やタンパク質分泌における翻訳後修飾の重要な過程の1つであり、こういった合成の大部分は粗面小胞体で行われる。

Q.立体選択性ってなに。

ある化学反応の生成物として複数の立体異性体が考えられる場合に、ある特定の立体異性体が優先的に得られる反応の性質についていう。

だそうです。

 

第8位

ウラムの螺旋らせん
［Ulam’s Spiral］

螺旋らせんって無条件にカッコいい。

アメリカのスタニスワフ・ウラムさんが発見。水爆の機構の発案者としても知られる。

ウラムの螺旋らせんとは、素数の分布をある簡単なルールに従って2次元平面に並べ、可視化したものである。

なるほど素数の分布図なわけか。初めて何となくわかるのが出てきたな。

 

これがウラムの螺旋らせんだ！

なにこれQRコード？

 

第7位

ディリクレのディオファントス近似定理
［Dirichlet’s approximation theorem］

ディオファントスだけでもカッコいいのに、その頭にディリクレって付いてるのがよりカッコよくて欲張り。

ドイツ人のヨハン・ペーター・グスタフ・ルジューヌ・ディリクレさんが証明した定理。名前ながっ！！

任意の実数α と 1 より大きい任意の自然数N に対し、分母が N 以下の自然数 q であるようなα の近似分数  で、 を満たすものが存在する。

わからないのは当然として、親戚の定理がいっぱいあるらしい。

 

（頭の悪い解説）

合ってる？ねぇこれ合ってるの？

 

第6位

グランドカノニカル・アンサンブル
大正準集団
［grand canonical ensemble］

物理用語です。FFの大技みたいでカッコいい。ネオエクスデス辺りが使ってきそう。

漢字パターンとカタカナパターン両方あるのがいいよね。気分によって使い分けられるし。

大正準集団とは、統計力学において、外界との間でエネルギーと物質を自由にやり取りできる開放系を無数に集めた統計集団である。

もはや惰性で置いてるだけの説明。

兄弟でミクロカノニカル・アンサンブルとカノニカル・アンサンブルもいるらしい。もうやめて。

 

閑話休題

ここで、いったん休憩。

数学豆知識でもご披露しましょう。

 

みんなが知らない！

関数グラフアートの世界～～！ﾊﾟﾁﾊﾟﾁﾊﾟﾁ！

 

y＝ax+bやy=ax²+bx+cといった関数をグラフに落とし込むことで、様々な曲線を描くことが可能なんですが。

これを利用した「関数グラフアート」という分野があり、全国コンテストが開かれているほどなんですね。

 

例えばこちら。

綺麗なハートがありますね。もちろん関数で描かれています。

 

ジャン！その際の数式がこちら！

いきなりxの8乗とか出てきてますが、こんなのはまだまだ序の口。

 

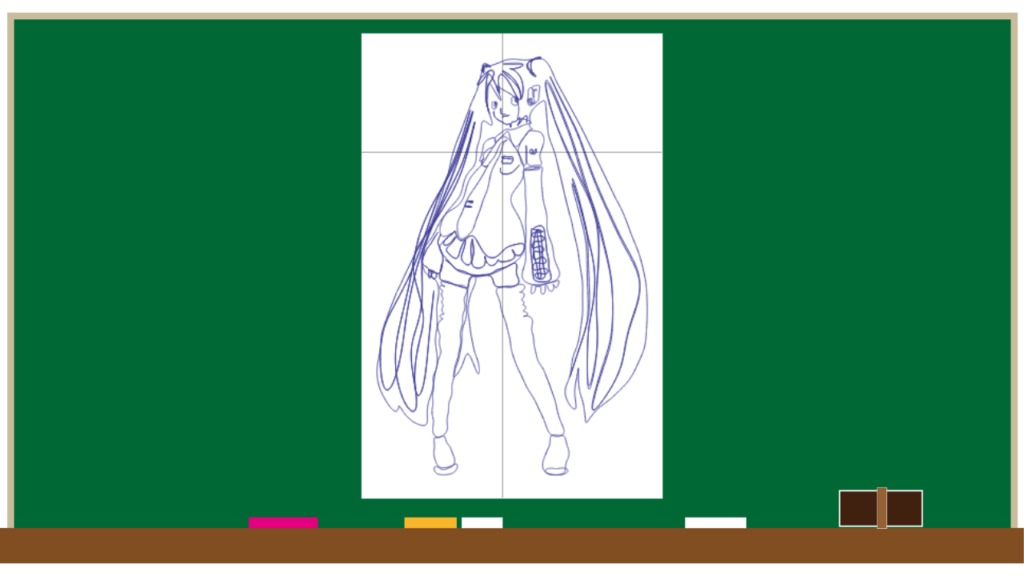
続いてはこちら。

何と、初音ミクが関数で描かれています。こんな複雑な曲線だらけ、一体どんな数式が使われてるんだ～！？

 

はいこちら！！！

これ8位のウラム螺旋らせんQRコードだろ。

 

いやいや、全部数式なんすよ、これ。

やばいとしか言いようがない。

 

最高に頭がおかしくなりそうになったところでランキングに戻ります！

 

第5位

ネイピア数の無理性の証明
［proof that e is irrational］

文節+文節+文節の組み合わせがカッコいい。「ネイピア」の響きもレイピアみたいでカッコいい。

スイス人のレオンハルト・オイラーさんが初めて行った証明だそう。

自然対数の底であるネイピア数 e は、2 < e < 3 を満たす無理数であり、背理法による証明で、すなわち、e が有理数であると仮定して矛盾を導いた。

うん。

 

これがレオンハルト・オイラーさんだ！

ちなみに、オイラーさんは右目を失明していたため「数学のサイクロプス（単眼の巨人）」と呼ばれていたんだとか。いちいちカッコいい。ムカついてきた。

 

第4位

スクーフ・エルキス・アトキン・アルゴリズム
［Schoof-Elkies-Atkin algorithm］

単語が4連続はさすがにカッコいい。声に出して言いたいカタカナ。

スクーフ・エルキス・アトキン・アルゴリズムとは、楕円曲線上の位数を計算し、順序集合を求める鍵生成アルゴリズムであり、ノアム・エルキスとA. O. L. アトキンによるスクーフ法の拡張理論である。

純度100％でわからん。わからなさすぎてもはやそれもカッコいい。

正直、wikiにもこれしか情報がなかったので何も言いようがない。

 

 

続いて第3位！

 

 

 

第3位

数論的双曲三次元多様体
［arithmetic hyperbolic 3-manifold］

漢字の塊でカッコいい。声に出して言いたい漢字。英語でちゃっかりハイパーボリックが入ってるのもカッコいい。

数論的双曲三次元多様体は、双曲三次元多様体であって、その基本群が PGL(2,C) の部分群として数論的群であるような多様体である。

さっきからずっと無知の知を自覚し続けてる。

これらの中で最も小さな体積の多様体は、ウィークス多様体であり、次に小さな体積の多様体はメイヤーホフ多様体である。

まず多様体がなにか教えて。お願い。

 

 

 

いよいよ第2位！

 

 

 

第2位

エラトステネスの篩ふるい
［sieve of Eratosthenes］

「篩ふるい」がシブくてカッコいい。賢者感があってカッコいい。

古代ギリシャ人のエラトステネスさんが考案したとされるそうな。

エラトステネスの篩ふるいは、指定された整数以下の全ての素数を発見するための単純なアルゴリズムである。

単純らしい。信用できん。

エラトステネスの篩ふるいは 以下の素数が既知のとき、( 以上）x 以下の素数を決定するには、x 以下の整数で  以下の素数の倍数を全て取り除けば（= 篩ふるえば）よいことを意味する。

は？単純って言ったよね？

このことから、

このことから？

包除原理を用いることによって x 以下の素数の個数に関する式を得ることができる。

知らん用語の補足に知らん原理を持ち出すな。そういうとこやぞ！バカ！

 

 

 

そして栄えある1位は…

 

 

 

 

第1位

次元の呪い
［the curse of dimensionality］

「次元」がカッコいい。「呪い」がカッコいい。シンプルでカッコいい。全てがカッコいい。

FF5のラストダンジョンってこんな名前じゃなかったっけ？あれ？違った？

アメリカ人のリチャード・アーネスト・ベルマンさんが使い始めた言葉らしい。

次元の呪いとは、（数学的）空間の次元が増えるのに対応して問題の算法が指数関数的に大きくなることを表している。

あ～～～ニュアンスは何となくわからんでもない。規模がデッカくなるとその分計算も大変になる的な…？

例えば、単位区間をサンプリングするには100個の点を等間隔で、かつ点間の距離を 0.01 以上にならないように配置すれば十分である。同じようなサンプリングを10次元の単位超立方体について行おうとすると、必要な点の数は 10²⁰ にもなる。したがって、10次元の超立方体はある意味では単位区間の10¹⁸倍の大きさとも言える。

矢継ぎ早にきた。

高次元ユークリッド空間の広大さを示す別の例として、単位球と単位立方体の大きさを次元を上げながら比較してみればよい。

よい。じゃねーよ。よい。じゃ。

高次元ユーグリッド空間ってどこにあんの？近所のコンビニにある？最寄りセブンなんだけど。

 

おわりに

ポスターにして部屋に貼りたい

いかがでしたでしょうか。

僕は短時間で『知』を摂取しすぎてもう爆発しそうです。

大正準集団な皆さんも、持ち前のファンデルワールス力でハイパーボリックに篩ふるっちゃってください。それでは、バッハハーイ！

 

おわり。

 

と言いたいところですが、せっかくなんで最後にイケてない用語も置いておきます。フェアじゃないからね、やっぱり。

それではダサい数学用語さん、バチッとお願いします！

 

 

 

参考サイト：

WolframeAlpha – 関数自動生成